Matenatika kelas 9
Persamaan dan Fungsi Kuadrat
1. Persamaan Kuadrat
Rumus
umum persamaan kudrat :
ax2
+ bx + c = 0
Contoh
persamaan Kuadrat
x2
+ 3x – 10 = 0
Carilah
akar – akar persamaan kuadrat diatas.
Jawab :
a. Cara Faktorisasi
Ini
adalah cara sederhana dalam menyelesaikan persamaan kuadrat.
Pertama
cari dua bilangan yang dijumlahkan menjadi 3 dan dikalikan menjadi
– 10
Kita coba
dengan angka 2, – 2, 5, – 5.
|
|
A |
B |
A + B |
A x B |
|
1 |
2 |
5 |
7 |
10 |
|
2 |
2 |
– 5 |
– 3 |
– 10 |
|
3 |
– 2 |
5 |
3 |
– 10 |
|
4 |
– 2 |
– 5 |
– 7 |
10 |
Lihat
table diatas ternyata nomor 3 yang memenuhi syarat penyelesaian persamaan
kuadrat tersebut yaitu – 2 dan 5.
Selanjutnya
masukkan kedua angka tersebut ke dalam persamaan :
x2
+ 3x – 10 = 0
( x – 2
)( x + 5 ) = 0
x1
– 2 = 0
x1 = 2
x2
+ 5 = 0
x1 = – 5
Jadi himpuan penyelesaiannya adalah {2, – 5}
b. Rumus ABC
Rumus ini
sangat universal karena bisa digunakan untuk semua bentuk persamaan kuadrat,
tanpa harus coba – coba seperti diatas,
Bentuk rumus ABC :
Contoh
penerapan rumus ini :
Misal
suatu persamaan kuadrat seperti ini
x2
+ 3x – 10 = 0
maka :
a = 1, b
= 3, c = – 10
Jadi himpuan penyelesaiannya adalah {2, – 5}
2. Grafik Fungsi Kuadrat
misal
persamaan Fungsi kuadrat y = x2
+ 3x – 10 atau bisa ditulis seperti ini
f(x) = x2 + 3x – 10 ,
Gambarkan
bentuk grafik fungsi kuadrat tersebut.!
Jawab :
Misal
kita mau membuat grafik fungsi kuadrat untuk rentang nilai x = 5 s/d x = – 5,
Lengkapi kolom – kolom di bawah ini , kita pilih nilai x sembarang,
|
x |
y = x2
+ 3x – 10 |
( x, y) |
|
5 |
30 |
(5, 30) |
|
3 |
8 |
(3, 8) |
|
1 |
– 6 |
(1, –
6) |
|
0 |
– 10 |
(0, – 10) |
|
– 1 |
– 12 |
(– 1, –
12) |
|
– 3 |
– 10 |
(– 3, –
10) |
|
– 5 |
0 |
(– 5,
0) |
Nilai
dari Hasil ( x, y) kemudian dipetakan ke grafik seperti dibawah ini :
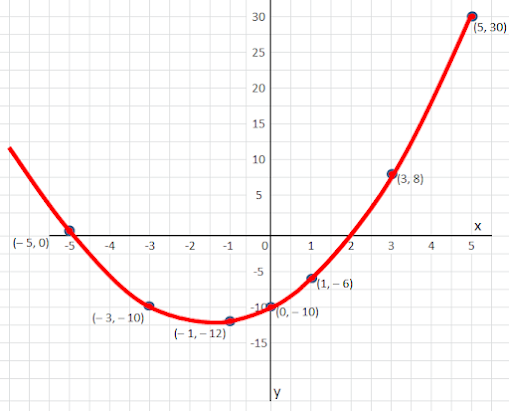 |
| Grafik fungsi y = x2 + 3x – 10 |
3. Sumbu Simetri dan Nilai Optimum
Sumbu
simetri dari Persamaan kudrat y = ax2
+ bx + c
adalah
Nilai y0 optimun :
Contoh
persaaan kuadrat
y = x2
+ 3x – 10
Tentukan
sumbu simetri dan nilai optimum persamaan tersebut
Jawab :
y = x2
+ 3x – 10
a = 1, b
= 3, c = – 10
1.
Sumbu simetrinya x adalah
2. Nilai y0 Optimum :
y0 = – 12,25
Sumbu
simetri dan nilai optimum bisa dilihat dari grafik di bawah
Sumbu
simetri (x = – 1,5) dan nilai y optimum (y0 = – 12,25)
Sehingga
titik optiumnya adalah (x, y) = ( – 1,5, – 12,25)
4. Menentukan Fungsi Kuadrat
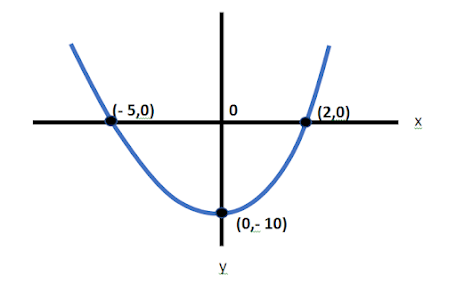
Diketahui
suatu garis lengkung memotong sumbu X di titik (– 5, 0)
dan (2, 0)
dan memotong sumbu Y di titik (0, – 10). Tentukan persamaan kuadrat garis
tersebut.
Jawab :
Rumus
umum persamaan kuadrat adalah y = ax2 + bx + c
Karena
memotong di sumbu x di titik (–
5, 0) dan (2, 0) maka persamaannya dapat ditulis sebagai berikut :
y = a(x +
5)(x – 2)
dan juga
memotong di sumbu y di titik (0, – 10) maka persamaan diatas dapat dirubah
menjadi :
– 10 =
a(0 + 5)(0 – 2)
⇔ a = – 10 / – 10 = 1
Sehingga
persamaan kuadrat dapat ditulis seperti ini
y = a(x +
5)(x – 2)
⇔ y = 1(x +
5)(x – 2)
⇔ y = x2
+ 5x – 2x + 5.( – 2)
⇔ y = x2 + 3x – 10
5. Aplikasi fungsi kuadrat
Contoh
penerapan rumus kuadrat di lapangan.
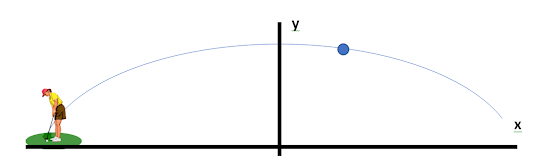
Seseorang
pemain golf memukul bola ke udara dengan sudut elevasi tertentu maka lintasan bola
tersebut merupakan lintasan persamaan kuadrat .
yang
mempunyai nilai tertentu
F(x) = ax2
+ bx + c atau dapat ditulis y = ax2
+ bx + c
Ketinggian
bola golf (Y) merupakan fungsi dari X (jarak
horizontal bola)
|
|
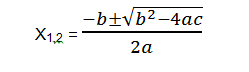


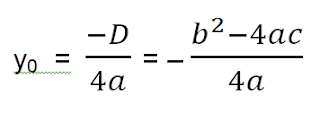
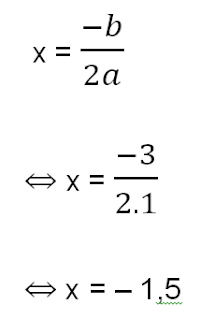
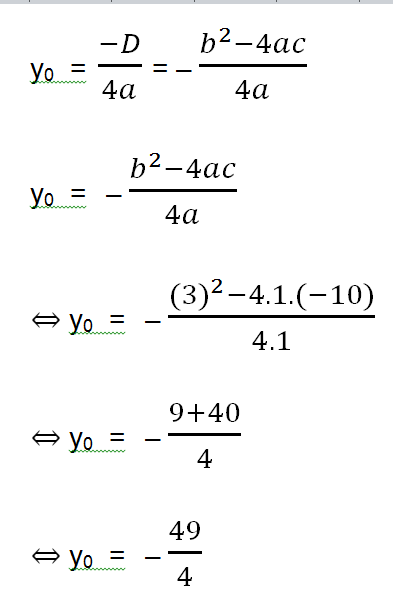

Tidak ada komentar:
Posting Komentar