Transformasi
A.
Pencerminan (Refleksi)
Pencerminan
adalah salah satu jenis transformasi yang menindahkan setiap titik pada suatu
bidang dengan menggunakan sifat bayangan cermin dari setiap titik yang
dicerminkan.
Koordinat
Bayangan hasil pencerminan (x, y)
|
No |
Pencerminan
Terhadap |
Titik
Koordinat Bayangan |
|
1 |
Sumbu-x |
(x, –y) |
|
2 |
Sumbu-y |
(–x, y) |
|
3 |
(0,0) |
(–x, –y) |
|
4 |
Garis y
= x |
(y, x) |
|
5 |
Garis y
= –x |
(–y, –x) |
|
6 |
Garis y
= h |
(x, 2h–y) |
|
7 |
Garis x
= h |
(2h–x, y) |
Contoh :
1.
Pencerminan terhadap sumbu x
Gambarkan segitiga ABC dengan A(-2,3), B(3, 1),
C(-2, 1) dan bayangannya terhadap sumbu x
Jawab :
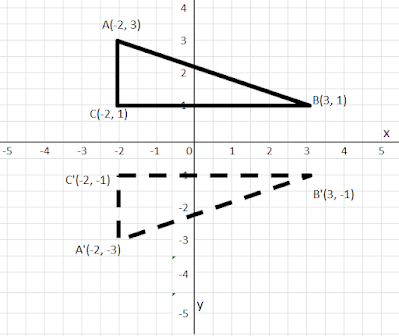 |
| Gambar pencerminan terhadap sumbu x |
2.
Pencerminan terhadap sumbu y

Gambar Pencerminan terhadap sumbu y
3.
Pencerminan terhadap titik pusat o (0, 0)

Gambar pencerminan terhadap titik pusat O(0, 0)
gambar diatas segitiga asalnya A(1, 3), B(5, 1),
C(1, 1) dicerminkan terhadap titik pusat o (0, 0) menghasilkan bayangan
segitiga A’(-1, -3), B’(-5, -1), C’(-1, -1)
4.
Pencerminan terhadap garis y = x
 |
| Gambar pencerminan terhadap garis y = x |
Gambar
diatas merupakan pencerminan segitiga A(1,-1), B(5, -3), C(1, -3) dicerminkan
terhadap garis y = x menghasilkan bayangan segitiga A’(-1,1), B’(-3, 5), C’(-3,
1)
5.
Pencerminan terhadap y = –x
 |
| Gambar pencerminan y = –x |
Diatas adalah pencerminan segitiga A(1,3), B(5, 1), C(1, 1) terhadap
garis y = –x menghasikan
bayangan A’(-3,-1), B’(-1, -5), C’(-1, -1)
6.
Pencerminan terhadap garis y =2
 |
| Gambar pencerminan terhadap garis y = 2 |
A’(1, -1), B’(5, 1), C’(1,
1)
7.
Pencerminan terhadap garis x =2
 |
| Gambar pencerminan terhadap garis x = 2 |
Gambar
diatas adalah contoh pencerminan segitiga A(5, 1), B(3, 1), C(5, 5) terhdap
garis x =2 yang menghasilkan bayangan segitiga
A’(-1,
1), B’(1, 1), C’(-1, 5)
B.
Pergeseran (Translasi)
Translasi
atau pergeseran adalah salah satu jenis transformasi yang memindahkan setiap
titik pada suatu bidang dengan arah dan jarak yang sama.
Contoh
translasi misalnya kamu memindahkan meja ke samping 2 m kemudian ke depan 3
meter. Ini berarti bahwa setiap titik pada bidang meja tersebut dipindahkan
dengan jarak dan arah yang sama yaitu ke samping 2 meter dan ke depan 3 meter.
Translasi pada bidang cartesius
dapat dinotasikan :
T = : P(x,y) → P'(x+a , y+b) artinya
meindahkan setiap titik P(x,y) dari sebuah bangun ke bidang P'(x+a , y+b).
Titik P’ adalah bayangn titik P oleh translasi T =
Contoh Soal :
Tentukan Bayangan segitiga A(-1,
1), B(1, 1), C(-1, 5) berikut oleh translasi
Jawab :
 |
| Gambar translasi |
Gambar
diatas menjelaskan translasi segitiga A(-1,
1), B(1, 1), C(-1, 5) oleh translasi
sehingga
diperoleh bayangan segitiga
A’(2, 3), B’(4, 3),
C’(2, 7)
C.
Perputaran(Rotasi)
Perputaran
adalh salah satu jenis transformasi yang memutar setiap titik Pada bidang
dengan sudut dan arah yang sama terhadap titik yang tetap. Besarnya sudut antara bayangan dengan bidang
awal merupakan sudut putar sedangkan titik tetap merupakan pusat rotasi.
Contoh
soal rotasi :
Tentukan
bayangan segitiga ABC dengan koordinat A(-1, 1), B(1, 1), dan C(-1, 5) diputar dengan sudut 900
berlawanan arah jarum jam dengan pusat rotasi titik (1, 0)
Jawab
: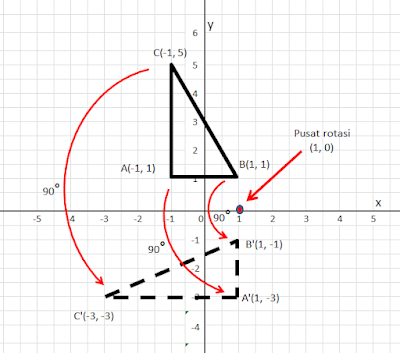
Gambar perputaran 900 ccw (Berlawanan Arah jarum jam)
Diatas adalh gambar yang menunjukkan jika segitiga ABC dengan koordinat A(-1, 1), B(1, 1), dan C(-1, 5) diputar 900 ccw
(Berlawanan Arah jarum jam)
akan menghasilakan bayangan segitiga A’B’C’ dengan koordinat A’(1, -3),
B’(1, -1), C’(-3, -3)
D.
Dilatasi
Dilatasi
merupakan salah satu jenis transformasi yang mengubah ukuran sebuah bangun
dengan titik pusat dan faktor skala tertentu.
Pada
dilatasi berlaku hal-hal berikut :
1. Dilatasi titik
A(x, y) dengan titik pusat O(0, 0) dengan factor skala k maka koordinat bayangannya
A’(kx, ky)
A(x, y) A’(kx,
ky)
2. Dilatasi
titik A(x, y) dengan titik pusat P(a, b) dengan factor skala k maka koordinat bayangannya A’(k(x – a) + a, k(x – b) + b)
A(x, y) A’(k(x – a) + a, k(x – b) + b)
atau bisa dinotasikan
A(x, y) A’(k(x – a) + a, k(x – b) + b)
Sifat – sifat dilatasi : :
ü JIka
nilai k > 1maka bangun tersebut diperbesar dan searah
dengan titik pusat P,
ü jika nilai k = 1 mka bangun tersebut tidak berubah.
ü Jika nilai 0 < k <
1 maka bangun tersebut diperkecil searah dengan titik pusat p,
ü jika nilai –1 < k < 0 maka bangun
tersebut diperkecil berlawanan dengan titik pusat
ü jika nilai k < – 1 maka bangun tersebut
diperbesar berlawangan dengan titik pusat
Contoh
soal :
Diketahui
segitiga ABC, dengan koordinat A(0.5, 1), B(0.5, 2), C(2, 1) diperbesar
(didilatasi) dengan factor skala k =
3 maka tentukan bayangan segitiga tersebut !
Jawab :
|
Koordinat Segitiga
ABC |
(kx, ky) |
Koordinat Segitiga
A’B’C” |
|
A(0.5, 1) |
(3x0.5, 3x1) |
A’(1.5, 3) |
|
B(0.5, 2) |
(3x0.5, 3x2) |
B’(1.5, 6) |
|
C(2, 1) |
(3x2, 3x1) |
C’(6, 3) |
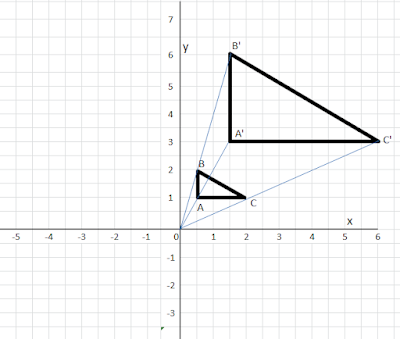
Gambar dilatasi segitiga ABC dengan factor skala k = 3